Decision Trees and Random Forests

What would you call the image below?

Would you say it’s a flowchart? Or a workflow? Or a brainstorm diagram? Or maybe even a web diagram? All of these names may fit depending on what is written inside each part of the diagram. However, data scientists will always call this a decision tree
Decision Tree Anatomy
Here is the same image as above, but color coded to highilight different parts of the anatomy.

In the diagram, each rectangle is called a node while each arrow is called an edge. There are three different types of nodes that are color coordinated on the image above. The blue node is called the root node. All data enters this node and is then sorted by the condition at the node. The orange nodes are internal nodes as they have edges both above and below. The green nodes are leaf nodes that represent possible outcomes or decisions that can be reached by using this tree.
Decision trees work just like you would expect from looking at the graph. For each observation, you start at the root node and follow the appropriate edges at each node. Using the example above, on a day where I do not have cereal and woke up late, I would skip breakfast. On a day where I had cereal, woke up an hour early, and had eggs I would make an omelette.
Decision trees are a useful model as they require no assumptions to be made about your data, and can be used in both regression and classification problems. This post will walk through some of the properties of decision trees and random forests, and walk through an example of implementing these models in python.
Decision Tree Properties
Advantages
- Not influenced by scale
- Not influenced by how data is distributed
- Don’t require special encoding
- Easy to interpret
Disadvantages
- High variance model that tends to overfit
Decision Tree Example
Before jumping into this example, you will need the following import statements. Please note that these statements are duplicated as comments in the code below so if you run this cell first you can ignore all subsequent import statements.
import pandas as pd
import numpy as np # This is optional
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split, cross_val_score
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier
If you do not have the scikit-learn, pandas, or numpy libraries installed, you can uncomment and run the necessary lines from the following code from your command line interface
# pip install sklearn
# pip install pandas
# pip install numpy
Loading in data
In this example I will be using the breast cancer dataset from scikit-learn. To load this dataset, run the following code:
# from sklearn.datasets import load_breast_cancer
data = load_breast_cancer()
For those unfamiliar with the scikit-learn library, datasets are saved as Bunch objects that contain multiple arrays. To get a clearer picture of the data we are working with, we can load our data into a pandas dataframe with the following code
# import pandas as pd
# Create a dataframe with the predictor variables and rename columns appropriately
df = pd.DataFrame(data.data, columns = data.feature_names)
# Add in column for y variable called 'target'
df['target'] = data.target
# Preview the first 5 rows of the dataframe
df.head()
| mean radius | mean texture | mean perimeter | mean area | mean smoothness | ... | worst compactness | worst concavity | worst concave points | worst symmetry | worst fractal dimension | target | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 17.99 | 10.38 | 122.80 | 1001.0 | 0.11840 | ... | 0.6656 | 0.7119 | 0.2654 | 0.4601 | 0.11890 | 0 |
| 1 | 20.57 | 17.77 | 132.90 | 1326.0 | 0.08474 | ... | 0.1866 | 0.2416 | 0.1860 | 0.2750 | 0.08902 | 0 |
| 2 | 19.69 | 21.25 | 130.00 | 1203.0 | 0.10960 | ... | 0.4245 | 0.4504 | 0.2430 | 0.3613 | 0.08758 | 0 |
| 3 | 11.42 | 20.38 | 77.58 | 386.1 | 0.14250 | ... | 0.8663 | 0.6869 | 0.2575 | 0.6638 | 0.17300 | 0 |
| 4 | 20.29 | 14.34 | 135.10 | 1297.0 | 0.10030 | ... | 0.2050 | 0.4000 | 0.1625 | 0.2364 | 0.07678 | 0 |
5 rows × 31 columns
Our goal in this problem will be to determine whether a given tumor is malignant or benign. The way this dataset was created, malignant tumors are labeled as 0, and benign tumors are labeled as 1. Since we are more interested in determining which tumors are malignant so we can recommend treatment begins immediately, we will switch these values using the code below.
# Switch values of 1 and 0 in df['target']
df['target'] = 1 - df['target']
# Preview first 5 rows to make sure change worked
df.head()
| mean radius | mean texture | mean perimeter | mean area | mean smoothness | ... | worst compactness | worst concavity | worst concave points | worst symmetry | worst fractal dimension | target | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 17.99 | 10.38 | 122.80 | 1001.0 | 0.11840 | ... | 0.6656 | 0.7119 | 0.2654 | 0.4601 | 0.11890 | 0 |
| 1 | 20.57 | 17.77 | 132.90 | 1326.0 | 0.08474 | ... | 0.1866 | 0.2416 | 0.1860 | 0.2750 | 0.08902 | 0 |
| 2 | 19.69 | 21.25 | 130.00 | 1203.0 | 0.10960 | ... | 0.4245 | 0.4504 | 0.2430 | 0.3613 | 0.08758 | 0 |
| 3 | 11.42 | 20.38 | 77.58 | 386.1 | 0.14250 | ... | 0.8663 | 0.6869 | 0.2575 | 0.6638 | 0.17300 | 0 |
| 4 | 20.29 | 14.34 | 135.10 | 1297.0 | 0.10030 | ... | 0.2050 | 0.4000 | 0.1625 | 0.2364 | 0.07678 | 0 |
5 rows × 31 columns
Next, set up our X and y variables and then train test split with the following code:
# from sklearn.model_selection import train_test_split
X = df[data.feature_names]
y = df['target']
X_train, X_test, y_train, y_test = train_test_split(X,
y,
stratify=y,
random_state=42)
In this particular dataset, the classes are slightly imbalanced as about 63% of the tumors are malignant (you can check this by running y.mean()). When we train/test split our data, we need to make sure to stratify by y in order to ensure both training and testing data have approximately the same percentage of observations in each class.
y.mean()
0.6274165202108963
X_train, X_test, y_train, y_test = train_test_split(X,
y,
stratify=y,
random_state=42)
Creating and fitting the model
# from sklearn.tree import DecisionTreeClassifier
tree = DecisionTreeClassifier(random_state=2)
Note that there are some parameters we can manipulate, but let’s start with the default decision tree model. I have added a random state to the model so that you can replicate the results of the code posted below.
We can use the cross-val-score module to predict how the tree will perform on testing data, and then actually fit and score the model using the train below.
# Print the cross validated score
print("Cross val score:",
cross_val_score(tree, X_train, y_train).mean())
# Fit the model to training data
tree.fit(X_train, y_train)
# Print the mean accuracy score on the testing data
print("Test data score:",
tree.score(X_test, y_test))
Cross val score: 0.9107981220657276
Test data score: 0.9370629370629371
The accuracy score of our model is approximately 93%. A pretty great start for a basic model. You may be wondering what this tree looks like. We can create a visual using the graphviz library. Please note, this can be difficult to install and may require other dependencies. I recommend using homebrew or a similar package management system to install this on your machine if you would like. Below you can see how this decision tree works.
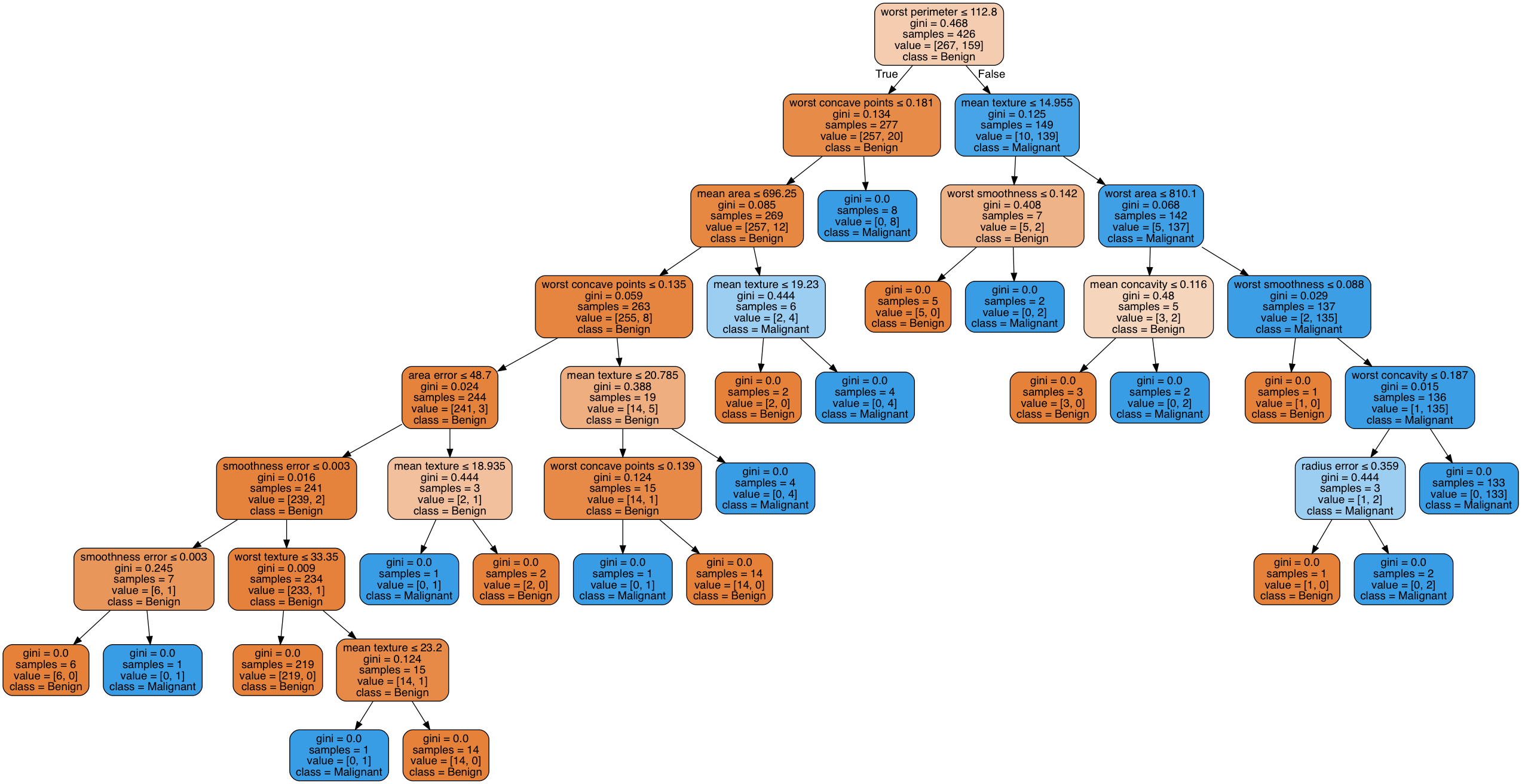 Visualization of the Decision Tree Created with the graphviz library
Visualization of the Decision Tree Created with the graphviz library
At this point, we may feel like we have created the best possible classification model. However, if you check the accuracy score against the training data using tree.score(X_train, y_train) you will see an accuracy score of 100%.
tree.score(X_train, y_train)
1.0
This discrepancy in our accuracy scores indicates that our model is overfit to the training data. This is something that decision trees are prone to. One way we can deal with this is by tweaking parameters within the decision tree like max_depth, min_samples_leaf, and min_samples_split.
The most powerful parameter in terms of addressing overfit is max_depth. This will determine the maximum number of times a split can occur before a node is deemed a leaf node. Decreasing this value will decrease the variance and overfit of your model, at the cost of increasing the bias in your model.
Another approach to dealing with overfit is to use ensemble methods like random forests.
Random Forests

Random Forest is a specific type of ensemble model. Ensemble models are essentially an amalgamation of models, often simpler or weaker models, that make predictions based on the predictions of its component models. The idea behind ensemble models is often referred to as “the wisdom of the crowd.” There are multiple examples of this phenomenon, and even a book written by James Surowiecki about it.
Basically, the idea boils down to the following: If you have enough people making guesses about a question, eventually the average of everyone’s guess will get pretty close to the actual answer. One of the examples linked above is about people guessing the weight of a cow from just a photograph, and with 17,000 responses the average guess of 1287 pounds was pretty close to the cow’s actual weight of 1355 pounds.
Random Forests use multiple decision trees in order to make more accurate predictions. However, simply making multiple decision trees from exactly the same training data would not be very effective, as the trees would have very similar predictions. This can be seen with the code below, which creates 2 decision trees with different random states and trains them on the same data.
# Create 2 decision trees with different random states
tree_1 = DecisionTreeClassifier(random_state=1)
tree_2 = DecisionTreeClassifier(random_state=2)
# Fit both trees to training data
tree_1.fit(X_train, y_train)
tree_2.fit(X_train, y_train)
# Make predictions based on the testing set
predictions_1 = tree_1.predict(X_test)
predictions_2 = tree_2.predict(X_test)
# Find how many differences there are in the
# predictions from each tree
# Create counter variable
differences = 0
# Iterate through all predictions
for i in range(len(predictions_1)):
# Increase count of differences when predictions are not the same
if predictions_1[i] != predictions_2[i]:
differences += 1
# Print number of differences and percent of differences
print(differences)
print(differences/len(predictions_1))
8
0.055944055944055944
Random Forests are a type of bagging (Bootstrapping + AGgregating) model. For each decision tree within the random forest, the tree will use a sample generated by bootstrapping from the training data set. Bootstrapping is sampling with replacement, an example of which can be seen below (please note this example is solely for explanatory purposes and is not necessary in creating the random forest model).
# import numpy as np
# Example of bootstrapping. This cell will return different
# values each time it is run.
my_list = [1, 2, 3, 4, 5]
np.random.choice(my_list, size=5, replace=True)
array([2, 1, 1, 4, 2])
The random forest separates itself from ordinary bagging models by introducing a max_features parameter, another aspect designed to differentiate each individual decision tree. Random forest models will restrict the number of features used to make a prediction at each node to the value of this max_features parameter. If you set max_features = 5, this means that at each node of each decision tree, the split will be based on a sample of 5 randomly selected features.
The algorithm will still locally optimize, but it will be limited to splitting based only on the value of the set of randomly selected features. This helps to differentiate the predictions from each individual decision tree. The random forest model will then use the predictions from all of its individual decision trees to make a prediction for each observation. The code below demonstrates how to instantiate, fit, and score using a random forest model.
# from sklearn.ensemble import RandomForestClassifier
# Instantiate model with default parameters and random state for replicability
rf = RandomForestClassifier(random_state=42)
# Print out cross validated scores to estimate performance
print("Cross val score:",
cross_val_score(rf, X_train, y_train).mean())
# Fit model to training data
rf.fit(X_train, y_train)
# Print accuracy score on testing data
print("Test data score:",
rf.score(X_test, y_test))
Cross val score: 0.948356807511737
Test data score: 0.951048951048951
Our random forest model had an accuracy score of approximately 95%, an improvement of about 2% on our solitary decision tree. We can tune some of the parameters of the random forest model in order to increase the accuracy of our model. One of the most powerful parameters is n_estimators, or the number of individual decision trees created within the model. The code below loops through different numbers of trees to include in the forest and prints the accuracy score on the testing set for each.
# Create list of values for the number of trees to include in the forest
num_of_trees = [1, 5, 10, 25, 50]
# Iterate through possibilities
for num in num_of_trees:
# Instantiate random forest model with appropriate number of trees
rf = RandomForestClassifier(n_estimators=num, random_state=3)
# Fit the model to the training data
rf.fit(X_train, y_train)
# Save score on testing set to variable score
score = rf.score(X_test, y_test)
# Print number of trees and score on testing set rounded to 4th decimal plance
print(f'With {num} trees the forest had an accuracy score of {round(score, 4)} on testing data')
With 1 trees the forest had an accuracy score of 0.9231 on testing data
With 5 trees the forest had an accuracy score of 0.9371 on testing data
With 10 trees the forest had an accuracy score of 0.9441 on testing data
With 25 trees the forest had an accuracy score of 0.958 on testing data
With 50 trees the forest had an accuracy score of 0.958 on testing data
From the output we can see that the accuracy score generally increased as the number of trees increased. If we wanted to find the optimal number of trees, we could use something like GridSearchCV from the sklearn.model_selection module.
One negative aspect about random forest models, and ensemble models more generally, is that they are difficult to interpret. However, with random forests we can use the attribute feature_importances_ to determine which features are most important in classifying each observation. The code below creates a pandas dataframe object with the feature importances labeled by the feature and sorted in descending order.
rf_50 = RandomForestClassifier(n_estimators = 50, random_state=3)
rf_50.fit(X_train, y_train)
feature_importances = pd.DataFrame(rf_50.feature_importances_,
index = X.columns,
columns = ['Importance'])
feature_importances.sort_values('Importance', ascending=False)
| Feature | Importance |
|---|---|
| worst perimeter | 0.175914 |
| worst concave points | 0.154266 |
| worst radius | 0.126445 |
| mean concave points | 0.089907 |
| worst area | 0.089881 |
| ". . ." | $\v |
| texture error | 0.004633 |
| mean fractal dimension | 0.003987 |
| concavity error | 0.003970 |
| smoothness error | 0.003730 |
| mean symmetry | 0.001063 |
There you have it. According to our random forest model with 50 trees, the three most important features in determining if a tumor is malignant are worst perimeter, worst concave points, and worst radius, while the three least important features are concavity error, smoothness error, and mean symmetry.